If a polynomial has real coefficients, and some of the roots are conplex, then the complex conjugate of each root is also a root.
To illustrate this for quadratis, notice that the roots of![]() are
are
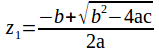 and
and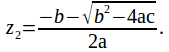
Since![]()
![]() and
and![]() are complex.
are complex.
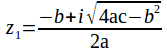 and
and![]()
Obviously![]() and
and![]()
This observation can be generalised to polynomials of any order with real coefficients. If![]() is a root of a polynomial then so is
is a root of a polynomial then so is![]()
Proof: Let![]() (1) with
(1) with![]() real.
real.
Let![]() be a root, then
be a root, then![]() (1)
(1)
Taking the complex conjugate gives![]() (2) (ince all the coefficients are real).
(2) (ince all the coefficients are real).
Obviously![]() is then also a root.
is then also a root.
Conversely suppose![]() and
and![]() are distinct roots.
are distinct roots.
![]() (3) and
(3) and![]() (4)
(4)
Taking the complex conjugate of the first one gives![]() (5)
(5)
(5) – (4) gives![]()
Taking the complex conjugate gives![]()
Adding gives![]() (6)
(6)
Divide by![]() and add to the complex conjugate. Do this repeatedly until you end up with
and add to the complex conjugate. Do this repeatedly until you end up with![]()
Repeat this process for decreasing powers of![]() to obtain
to obtain![]() for all
for all![]()