If a function is one to one, so that every value in the domain is associated with a unique value in the codomain and every value in the codomain is associated with a unique value in the domain, then the function can be inverted.
An invertible function can have no turning points (minima or maxima). The gradient must always have the same sign, and if it is zero, can only be zero at a single point on any interval. That is, the function must be always either increasing or decreasing.
![]() and
and![]() are invertible function. In fact they are inverses of each other so that
are invertible function. In fact they are inverses of each other so that![]() and
and![]() The graphs of
The graphs of![]() and
and![]() are shown below. Each is the reflection of the other in the line
are shown below. Each is the reflection of the other in the line![]()
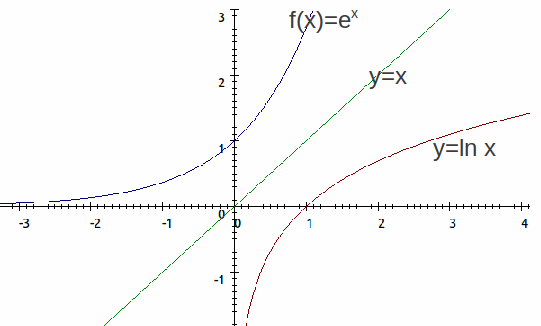
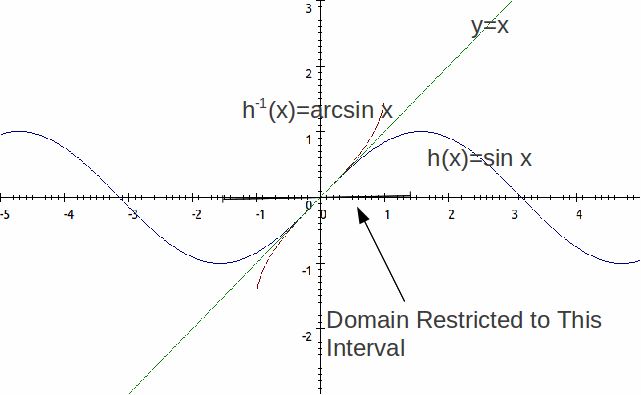
We can often make a non – invertible function invertible by restricting the domain. For example,![]() is non invertible because it is not one to one:
is non invertible because it is not one to one:![]() for all
for all![]() We can however, make it invertible by restricting the domain to
We can however, make it invertible by restricting the domain to![]() so that the function is one to one on that domain, then it will be invertible with that restriction.
so that the function is one to one on that domain, then it will be invertible with that restriction.
There is a procedure for finding the inverse of a one to one function![]()
-
Make
 the subject.
the subject. -
Interchange
 and
and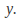
-
Replace
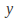 with
with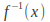
For example, if![]() then applying step 1 gives
then applying step 1 gives![]()
Now apply step 2 to get![]()
And finally step 3 to get![]()