Transforming functions is related to the transformation of graphs. A function is basically a sequences of operations on some argument. The argument can be anything, but whatever the argument is, the function does the same sequence of operations, in th same order, to each argument. Suppose that the function f says, 'square the argument'.
We can also write![]() where it is understood that
where it is understood that![]() is the argument.
is the argument.
For this example,![]()
Suppose now that the argument is not![]() but some other expression in
but some other expression in![]() say
say![]()
![]() says 'square 3x+1
says 'square 3x+1![]() so that
so that![]()
This definition of a function is precisely consistent with the transformation of a graph. Continuing with the example above,![]() suppose we replace the argument
suppose we replace the argument![]() by
by![]() so that
so that![]() If we were to transform the graph of
If we were to transform the graph of![]() to obtain the graph of
to obtain the graph of![]() we would scale the
we would scale the![]() – axis by a factor of
– axis by a factor of![]() When we transform a function however, instead of labelling the x – axis as the x – axis, we label it as the
When we transform a function however, instead of labelling the x – axis as the x – axis, we label it as the![]() axis. To relabel it the
axis. To relabel it the![]() – axis, we have to divide all the
– axis, we have to divide all the![]() – values on the axis by 2 which is the same as scaling by a factor of
– values on the axis by 2 which is the same as scaling by a factor of![]()
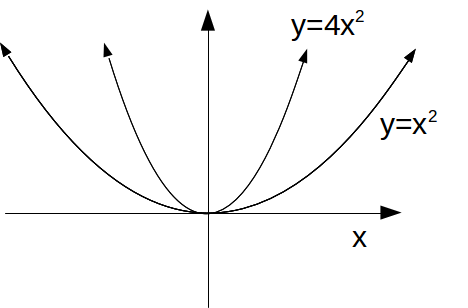
In general, when transforming a function by changing the argument, we can just relabel the![]() – axis. To maintain the
– axis. To maintain the![]() – axis as the
– axis as the![]() – axis, we are required to perform the inverse sequence of operations that turned
– axis, we are required to perform the inverse sequence of operations that turned![]() into '
into '![]() ' or '
' or '![]() ' or whatever the new argument is.
' or whatever the new argument is.