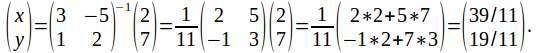The simultanous equations
x+2y=5
x-y=2
has the unique solution x=3, y=1.
We can write the system in matrix form as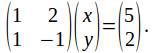
Then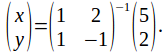
The condition nexcessary for a unique solution to exist is then that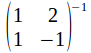
exists, OR, since
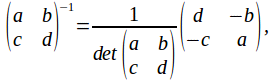that
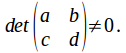
We can generalize this.
If a system of linear equations can be associated with a square coeefficient matrix with non zero determinant, then the system has a unique solution. More specifically, if we can write a system of linear equations in the form
where
is a square matrix and
is the vector of variables to be solved for, then
Example: Find if the system of equations
has a unique solution, and if so find it.
The third equation is reduncant, since it is twice the second equation. The system is equivalent to the system
The coeefficient matrix is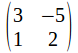
with determinant
so the system has a unique solution, given by
