Standard, Deviation, Variance and Bias
Given a flock of sheep, we can measure the masses of a sample of sheep and calculate the mean mass and the standard deviation of the masses of the sheep in the sample.
Suppose the masses of the sheep are
50, 55, 52, 60, 54, 49, 59, 58
The sample mean is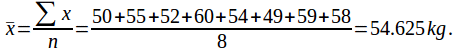
The sum of the squares of the masses is![]()
The variance of the sample, called the sample variance is then and the sample standard deviation
and the sample standard deviation![]()
This is not that same as the variance of the masses of the whole population of sheep in general, and is not even a very good estimate.