90% of infected people test positive.
10 of infection free people test positive.
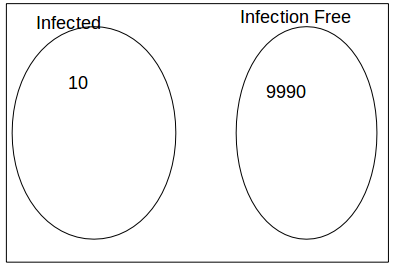
We are interested in the probability that a person who test positive is infected. Of 10,000 people, 10 will be infected on average and 99,990 will be infection free..
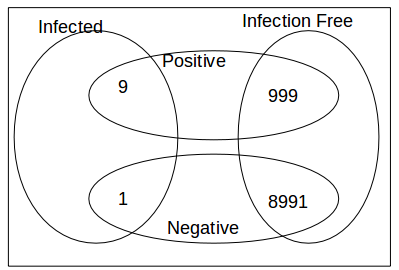
The probability of actually being infected when you test positive is only
\[\frac{9}{9+999}=\frac{1}{112}\]
.