Induction With Matrices
Many properties of matrices of presereved by matrix multiplication.
If square diagonal matrices are multiplied (diagonal means that entries on the leading diagonal are non zero eg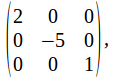 the result is a diagonal matrix.
the result is a diagonal matrix.
If upper triangular matrices – example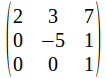 - are multiplied, the result is an upper triangular matrix and if lower triangular matrices are multiplied, the result is a lower triangular matrix.
- are multiplied, the result is an upper triangular matrix and if lower triangular matrices are multiplied, the result is a lower triangular matrix.
Matrix proofs using induction often deal with powers of matrices.
If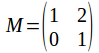 then
then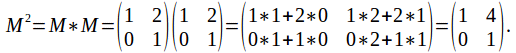
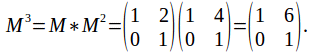
If![]() then entry in the upper right corner of
then entry in the upper right corner of![]() is 2 and the diagonal entries are 1.
is 2 and the diagonal entries are 1.
If![]() then entry in the upper right corner of
then entry in the upper right corner of![]() is 4 and the diagonal entries are 1.
is 4 and the diagonal entries are 1.
If![]() then entry in the upper right corner of
then entry in the upper right corner of![]() is 5 and the diagonal entries are 1.
is 5 and the diagonal entries are 1.
We might speculate that the entry in the upper right corner of![]() is
is![]() and and the diagonal entries are 1 and we can prove this by induction. Suppose
and and the diagonal entries are 1 and we can prove this by induction. Suppose![]() is the statement ' the entry in the upper right corner of
is the statement ' the entry in the upper right corner of![]() is
is![]() '.
'.
If![]() the upper right entry is 2 and the diagonal entries are 1 so the basis step is true.
the upper right entry is 2 and the diagonal entries are 1 so the basis step is true.
Suppose P(n) is true so that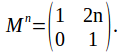
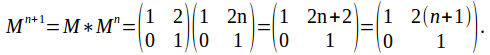
![]() is true so the staement is proved by induction.
is true so the staement is proved by induction.