The simplest prrof by induction involve finding a simple formula for the nth term of a sequence.
Proofs by induction have three parts.
1. Asume![]() is true. Often
is true. Often![]() or 1 so we are assuming
or 1 so we are assuming![]() or
or![]()
![]() could be the statement that the nth term of a sequence is some formula for that nth term – for example, the nth even number is
could be the statement that the nth term of a sequence is some formula for that nth term – for example, the nth even number is![]() so
so![]() is the statement that the first even number is 2.
is the statement that the first even number is 2.
2. Assume![]() is true for some
is true for some![]()
3. Prove![]() is true.
is true.
For the simple example above,
![]() is true since the first even number is 2.
is true since the first even number is 2.
If![]() is true then the nth even number is
is true then the nth even number is![]()
Given an even number, to find the succeeding even number, add 2, so the (n+1)th even number is![]() so that
so that![]() is true.
is true.
Example: Prove that the sum of the first![]() numbers is
numbers is![]()
![]() is the statement that the sum of the first 1 numbers is 1. Obviously this is true. Substitute
is the statement that the sum of the first 1 numbers is 1. Obviously this is true. Substitute![]() into (1) to give
into (1) to give![]() so
so![]() is true.
is true.
Assume![]() is true for some
is true for some![]() so that the sum of the first n numbers is
so that the sum of the first n numbers is![]()
The (n+1)th number is![]() We can add this to the sum of the first
We can add this to the sum of the first![]() numbers to get the sum of the first
numbers to get the sum of the first![]() numbers.
numbers.
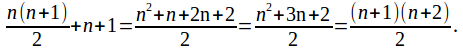
The statement![]() is the statement that the sum of the first
is the statement that the sum of the first![]() numbers is
numbers is![]() so that
so that![]() is true.
is true.