Relation Between Angles in Adjacent Triangles Problem
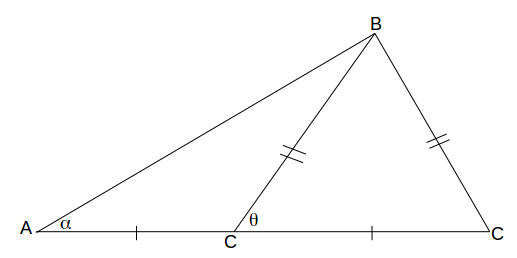
In the triangle below\[AD=CD, \: BD=BC\]
. The problem is to find a relationship between \[\alpha\]
and \[\theta\]
.
\[\alpha\]
and \[\theta\]
.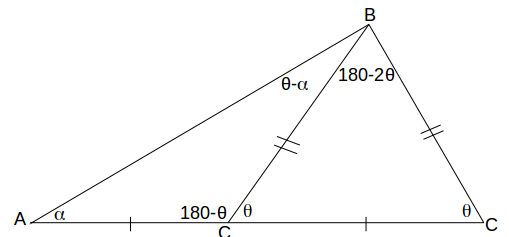
\[\frac{sin \alpha}{BD}=\frac{sin(\theta - \alpha )}{AD} \rightarrow \frac{AD}{BD}=\frac{sin (\theta - \alpha )}{sin \alpha}\]
and again on triangle BCD.
\[\frac{sin (180- \theta )}{CD}=\frac{sin(\theta }{BD} \rightarrow \frac{CD}{BD}=\frac{sin (180 -2 \theta )}{sin \theta}\]
\[AD=CD\]
so \[\frac{sin (\theta - \alpha )}{sin \alpha}=\frac{sin (180 -2\theta )}{sin \theta}\]
Use the identities
\[sin(\theta - \alpha)=sin \theta cos \alpha - cos \theta sin \alpha\]
and \[sin(180-2 \theta )=sin 2 \theta = 2 sin \theta cos \theta\]
to get\[\frac{sin \theta cos \alpha - cos \theta sin \alpha}{sin \alpha}= \frac{2 sin \theta cos \theta}{sin \theta}\]
\[sin \theta cot \alpha - cos \theta = 2 cos \theta\]
\[sin \theta cot \alpha = 3 cos \theta\]
\[tan \theta cot \alpha = 3 \rightarrow tan \theta = 3 tan \alpha\]