A line, which is a two dimensional object, is fixed by two points on it – two dimensions, two points. The equation of a line can be written given by![]() – this is the cartesian form of the line. The cartesian form of a plane is
– this is the cartesian form of the line. The cartesian form of a plane is![]() where
where![]() and
and![]() are constants To find the equation of a plane we need three points. Each point determines an equation in
are constants To find the equation of a plane we need three points. Each point determines an equation in![]() We solve these simultaneous equations to find the constants
We solve these simultaneous equations to find the constants![]() in terms of
in terms of![]() and write down the equation of the plane. Finally we cancel the constant d which appears throughout.
and write down the equation of the plane. Finally we cancel the constant d which appears throughout.
Example: A plane passes through the three points![]() and
and![]() Find the equation of the plane.
Find the equation of the plane.
Substituting the first point![]() into the equation of the plane
into the equation of the plane![]() gives
gives
![]()
Similarly the second and third give![]() and
and![]() We solve the simultaneous equations,
We solve the simultaneous equations,
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
(1)+(3) gives![]()
Sub![]() into (2) to give
into (2) to give![]()
Sub![]() and
and![]() into (1) to give
into (1) to give![]()
The equation of the plane is then![]() Cancel the factor
Cancel the factor![]() to give
to give![]() and clear all the fractions to give the final answer
and clear all the fractions to give the final answer![]()
There is an alternative form for the equation of a plane to terms of vectors:![]() where
where![]() and
and![]() are parameters and
are parameters and![]() is a point in the plane. For the plane give above we can find
is a point in the plane. For the plane give above we can find![]() and
and![]() by subtracting points in the plane from each other:
by subtracting points in the plane from each other:
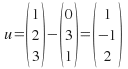 and
and 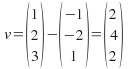
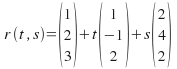 .
.
The vector form is not unique since any points in the plane can be used.