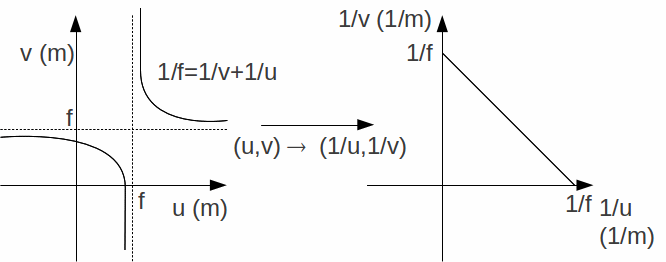Choosing Variables For a Straight Line

Not every equation naturally gives rise to a straight line. If we have variablesandrelated byorandrelated bythen graphs ofagainstoragainst will not result in a straight line. We are however not restricted to plotagainstor againstWe can often rearrange an equation into a form which will give a straight line if we plot a suitable function of one variable against a suitable function of the other. In order to do this we need to:

• Identify which symbols in the equation are variables and which are constants.

• The symbols that correspond to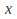and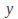must be variables and the symbols that correspond to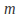and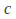must be constants.

• If a variable is cubed, square rooted or the reciprocal, log or exponential is taken, the result is still a variable and may still be used to label one of the axes.

• Any function of the readings may be used to label the axes, since the result is still a variable.

• Sometimes the physical quantities use the same symbols as in our notation e.g.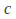is used to denote the speed of light. Do not get these confused.

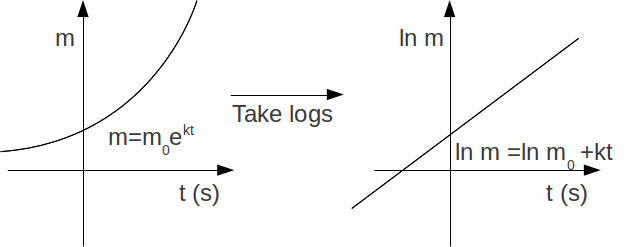
For the equationabove, taking natural logs results in a straight line.

For the equationabove, plottingagainstresults in a straight line with gradient -1 andinterceptsince