Linear Momentum – units kg m/s - is defined as the product of mass and velocity. It is a vector, and is of fundamental importance because in any collision or any isolated system it is conserved as a consequence of Newton's third law.
We can write this conversation law for two masses![]() and
and![]() with initial velocities
with initial velocities![]() and
and ![]() and final velocities
and final velocities![]() and
and![]() respectively as
respectively as
![]()
This can be rearranged as
![]()
or![]()
The impulse given to a body as a result of an interaction of some sort with another is written as![]() so we can see from the last expression above that the impulses that bodies exert on each each other are equal and opposite. This is an expression of Newton's third law.
so we can see from the last expression above that the impulses that bodies exert on each each other are equal and opposite. This is an expression of Newton's third law.
We can write the force exerted on a body as![]() Integration of this with respect to
Integration of this with respect to![]() gives
gives![]() If
If![]() is constant then
is constant then![]() so we may consider an impulse as due to a force
so we may consider an impulse as due to a force![]() applied for a time
applied for a time![]()
Example: A jet of water leaves a hose at the rate of![]() per second at a speed of 20 m/s. It hits a wall and is brought to rest. Find the force exerted by the jet on the wall.
per second at a speed of 20 m/s. It hits a wall and is brought to rest. Find the force exerted by the jet on the wall.
The force exerted on the wall equals the rate of change of momentum of the water. In one second a mass of water equal to density*volume=1000*0.005=5 kg hits the wall. This water has momentum equal to 5*20=100 kg m/s. Since this water is brought to rest every second, the force exerted on the wall is 100 N.
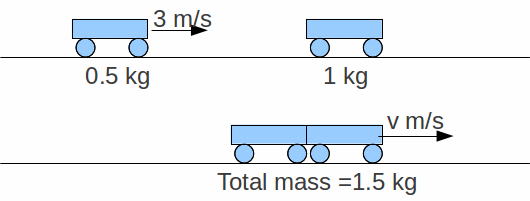
Example: A toy truck of mass 0.5 kg moving at a speed of 3 m/s collides with a stationary truck of mass 1 kg. The trucks stick together during the collision and afterwards move as one. Find their common velocity after the collision.
Initial momentum![]()
Hence final momentum