The Schrodinger Model
Edwin Schrodinger built on the de Broglie hypothesis that matter could behave as waves and used it to propose an alternative model of the hydrogen atom. In Schrodinger's model the wavefunction may take different forms, depending on the energy of the electron. Only a few possible wavefunctions for each particular energy fit the boundary conditions – that a whole number of wavelengths can fit into an orbit, and that as the radius tends to infinity, the wavefunction must tend to zero. As in the Bohr model, an electron at the nth energy level, has an energy of![]() but is position at any time is not certain. The probability of find the electron is any small volume
but is position at any time is not certain. The probability of find the electron is any small volume![]() is given by
is given by![]()
Graphs of![]() against
against![]() the distance from the nucleus are given below for various energy level various values of angular momentum, indicated by the letter s,pd,f etc are shown below.
the distance from the nucleus are given below for various energy level various values of angular momentum, indicated by the letter s,pd,f etc are shown below.
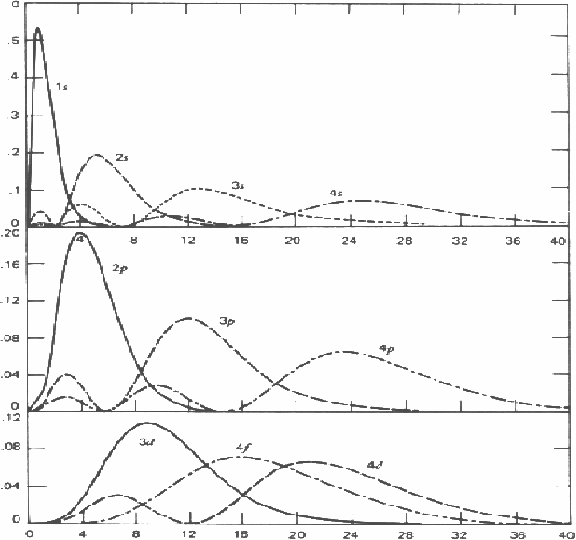
Notice that each wavefunction tends to zero as r tends to infinity. As the angular mometum increases from zero, indicated by s, by one unit successively, (p,d,f..) there appear values of r for which the wavefunction is zero, indicating the electron may not be found at theose values of the radius.