Standing Waves on Strings
A standing wave occurs when a wave is confined in space. Repeated reflections occur from the walls of the space that confines the wave. For certain frequencies the time taken for a wave to travel back and force between the interval of confinement equals the time taken to produce another oscillation. In this case constructive interference will occur. If the lowest frequency at which a standing wave is produced is called f then standing waves are produced at all integer multiples of f. Standin waves are only produced for multiples of f because this is the
The diagram below illustrates the production of standing waves on strings. The left hand side is moved up and down and the right and side of the string is fixed. In the time it takes fro the left hand side of the string to move up and down once, (fundamental), twice (First overtone), three times (Second Overtone), three times (third overtone) etc the waves travel to the right hand fixed point and back. In this way constructive interference occurs.
The strings below oscillate up and down. At the start of a cycle for example the string is shown in red, and half a second later in blue.
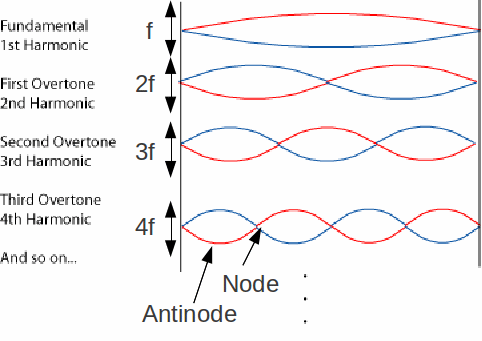
There are some points along the string where no vibration occurs. These are called nodes. At these points complete destructive interference occurs between the reflected wave on the string travelling to the left and the wave on the string travelling to he right. At other points, called antinodes, constructive interference occurs and there is maximum displacement.