Perimeter of an n Sided Polygon Inscribed in a Circle
The angle at the centre of a isosceles triangle formed by the sides of n - sided regular polygon inscribed in a circle is and lines drawn from the centre to consecutive vertices is\[\frac{2 \pi}{n}\]
.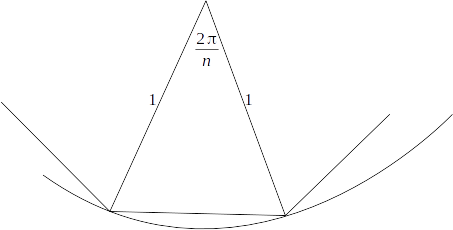
\[a= \sqrt{1^2 +1^2 - 2 \times 1 \times 1 \times cos \: ( \frac{2 \pi}{n})} = \sqrt{2 -2 cos \: ( \frac{2 \pi}{n})} = \sqrt{2} \sqrt{2} sin \: (\frac{2 \pi}{n}) = 2 sin \: ( \frac{\pi}{n})\]\]
The perimeter of the n - sided polygon is then
\[n \times sin \: ( \frac{\pi}{n})\]
As
\[n \rightarrow \infty , n \times sin \: ( \frac{\pi}{n}) \rightarrow n \times \frac{ 2 \pi}{n} = 2 \pi\]