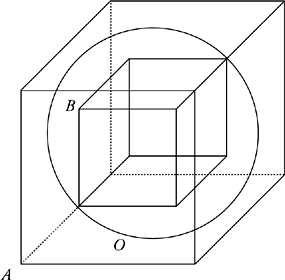
Suppose a cube is placed inside a sphere so that the vertices of the cube just touch the sphere. The sphere is placed inside a cube so the sphere just touches the centre of each face of the cube.
 \[2x\]
\[2x\]
the its volume is
\[(2x)^3=8x^3\]
.
The distance from the centre of the innermost cube to a vertex of the cube is equal to the radius of the circle and is
\[\sqrt{x^2+x^2+x^2} = x \sqrt{3}\]
.
The side of the large cube is twice the radius of the sphere, and is equal to
\[2x \sqrt{3}\]
Then
\[\frac{Volume \: of \: Large \: Cube}{Volume \: of \: Small \: Cube}= \frac{(2x \sqrt{3})^3}{8x^3} = 3 \sqrt{3}\]
 \[2x\]
\[2x\] \[2x\]
\[2x\]