Transformations of Graphs
We can sort transformations of graphs into two types -x transformations or y transformations. Anything else is a combination of an x transformation followed by a y transformation or vice versa.
A transformation is an x transformation if it is an argument of a function on the right hand side, or if it can be written in brackets without looking like nonsense. For instance, these are some x transformations:
![]()
x transformations are always counter – intuitive..To transform![]() you might think you scale by 2 in the x direction. THIS IS WRONG!!! You scale by
you might think you scale by 2 in the x direction. THIS IS WRONG!!! You scale by![]() Your graph becomes compressed in the x – direction, not expanded. And to transform
Your graph becomes compressed in the x – direction, not expanded. And to transform![]() you do not subtract 2 from all the x's, hence moving the graph left. You add 2 to all the s's and move the graph right.
you do not subtract 2 from all the x's, hence moving the graph left. You add 2 to all the s's and move the graph right.
Y transformations are easier.![]() implies correctly, a scaling by 2 in the y direction. Notice the difference between sin2x or sin(2x) which is an x transformation and 2sinx , which is a y transformation. These are some more examples of y transformations:
implies correctly, a scaling by 2 in the y direction. Notice the difference between sin2x or sin(2x) which is an x transformation and 2sinx , which is a y transformation. These are some more examples of y transformations:
![]()
y transformations are always intuitive. To transform![]() you move the graph up 1, and for
you move the graph up 1, and for![]() we scale by 4 in the y direction.
we scale by 4 in the y direction.
Sometimes we can have a combination of transformations:
![]() represents a scaling by 3 in the y direction FOLLOWED by a movement up 2. It would be wrong to do it the other way round.
represents a scaling by 3 in the y direction FOLLOWED by a movement up 2. It would be wrong to do it the other way round.
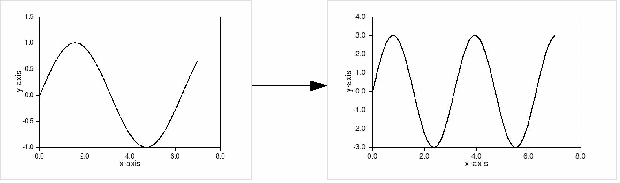
![]() represents a scaling of 3 in the y direction and a scaling by
represents a scaling of 3 in the y direction and a scaling by![]() in the x direction. This is illustrated above.
in the x direction. This is illustrated above.