Any expression of the form![]() is a difference of squares and factorises:
is a difference of squares and factorises:
![]()
For example, if![]() then
then![]() and
and![]() (note we always take the positive square root) so
(note we always take the positive square root) so![]()
Sometimes we need to factorise with any common factors before we can use the difference of squares factorisation.
![]()
Now put![]() so that
so that![]() and
and![]()
![]()
The roots of the difference of squares![]() is the set of values of
is the set of values of![]() for which
for which![]() The roots are always equal in magnitude and opposite in sign. If an quadratic expression factorises into a difference of squares this is always the case. If we sketch this function, it is a quadratic graph with the line of symmetry
The roots are always equal in magnitude and opposite in sign. If an quadratic expression factorises into a difference of squares this is always the case. If we sketch this function, it is a quadratic graph with the line of symmetry![]() and minimum at
and minimum at![]()
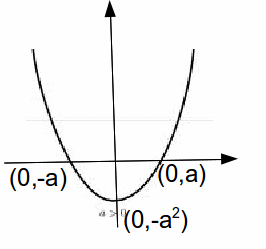
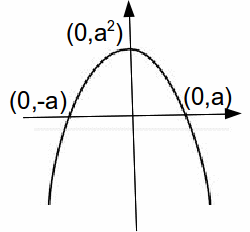
The roots of the difference of squares![]() are x=-a and x=a. If we sketch this function, it is a quadratic graph with the line of symmetry
are x=-a and x=a. If we sketch this function, it is a quadratic graph with the line of symmetry![]() and minimum at
and minimum at![]() This is a 'sad' curve, as opposed to the 'happy' curve above.
This is a 'sad' curve, as opposed to the 'happy' curve above.
The above examples are quadratics, with![]() terms but this need not be the case.
terms but this need not be the case.
![]()
![]()
![]()