An Embedded Process
Suppose we have a birth and death process. The rate at which births occur is![]() and the rate at which deaths occur is
and the rate at which deaths occur is![]() Sometimes we are not interested the time of a particular process but only in whether it is a birth or a death. We can relabel the time of the ith change as
Sometimes we are not interested the time of a particular process but only in whether it is a birth or a death. We can relabel the time of the ith change as![]() and obtain a random process
and obtain a random process![]() Time has been made discrete. The process is said to be embedded in the original process and
Time has been made discrete. The process is said to be embedded in the original process and![]() is the size of the population immediately after the ith change.
is the size of the population immediately after the ith change.
For the simple birth and death process the probability of a birth is![]() and the probability of a death is
and the probability of a death is![]()
This means that we have a simple random walk with![]() and
and![]()
If x ever becomes zero, it stays zero permanently and the population is extinct. The problem is now a gambler's ruin problem. Using results from the gambler's ruin problem we can say that if the initial population is x_0 then the probability of extinction is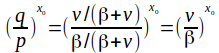 if
if![]() and 1 if
and 1 if![]()
The expected number of points (births and deaths) before the population goes extinct is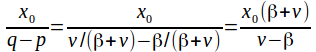 if
if![]() The expected time to extinction is infinite if
The expected time to extinction is infinite if![]()