If a resultant force acts on a body initially at rest, the speed of the body will increase. The force will do work on the body. If there is no resistance to motion, all the work done by the force will be expressed in an increase of kinetic energy of the body.
If the force![]() is constant then Newton's Second Law of motion,
is constant then Newton's Second Law of motion,![]() tells us that the acceleration will be constant. The work done is the force mult0lied by the distance moved,
tells us that the acceleration will be constant. The work done is the force mult0lied by the distance moved,![]()
Using Newtons second law in this equation for the work done gives
![]()
Now we can use one of the equations of motion,![]() Since the body starts from rest,
Since the body starts from rest,![]() so
so![]()
Substitute this expression into the formula for the work done to give![]()
Problems can often be solved using either the equations of motion for uniform acceleration or by assuming energy is conserved and equation the initial to the final energy. Suppose for example that a ball is thrown up in the air with a speed of 20 m/s. . We want to find the maximum height of the ball. Gravity will cause it to decelerate down with an acceleration of -9.8 m/s 2 (negative since down). Using SUVAT gives
![]()
![]()
![]()
![]()
![]()
![]()
Equating the initial kinetic energy to the graviational potential energy at the maximum height gives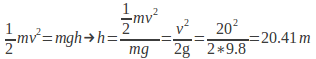
as before.