Any expression of the form![]() cannot always be factorised as with simple quadratics, by finding factors of c. Instead there is a slightly more complicated procedure, best illustrated by an example:
cannot always be factorised as with simple quadratics, by finding factors of c. Instead there is a slightly more complicated procedure, best illustrated by an example:
Factorise![]()
-
Take out any common factor. Every term in the above expression has a factor 3, so we may write the expression as
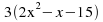
-
Multiply the coefficient of
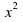 by the constant term:
by the constant term: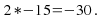 Find the two factors of this product which add to give the coefficient of
Find the two factors of this product which add to give the coefficient of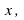 which in this case is -1.
which in this case is -1. -
Rewrite the term in brackets using these two factors:
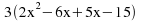
-
Take out common factors for each pair:
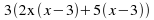
-
Factorise completely:
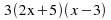
Example
Factorise![]()
-
Take out common factors:
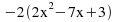
-
Multiply the coefficient of
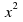 by the constant term:F
by the constant term:F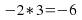 ind the two factors of this product which add to give the coefficient of
ind the two factors of this product which add to give the coefficient of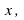 which in this case is -7: -1 and -6.
which in this case is -7: -1 and -6. -
Rewrite the term in brackets using these two factors:
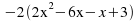
-
Take out common factors for each pair:
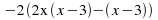
-
Factorise completely:
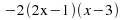
Differences of Squares
Any expression of the form![]() can be factorised almost instantly:
can be factorised almost instantly:![]()
Example:![]()
Example:![]()