Curves - Maxima, Minima, Stationary Points and Turning Points
I don't know why these thing need four possible names. We can call them stationary points and classify them as maxima or minima.
Definition: A stationary point is a point on a curve where![]()
Definition: A stationary point, with![]() is a Minima if
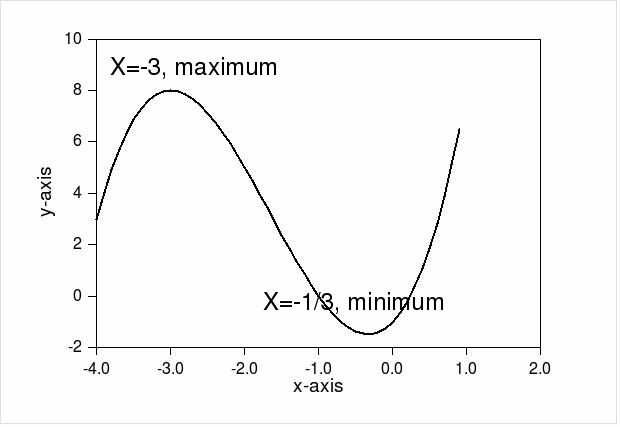
is a Minima if![]() On a graph a minimum is lower than the points on either side as on the graph below.
On a graph a minimum is lower than the points on either side as on the graph below.
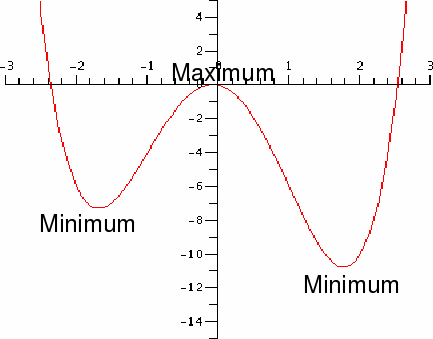
Definition: A stationary point, with![]() is a Maxima if
is a Maxima if![]() A maximum is above the points on either side of it.
A maximum is above the points on either side of it.
We often have to find the stationary points and classify them as maxima or minima. To do this,
We find
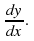 and solve
and solve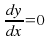 to find the x – coordinates of the turning points.
to find the x – coordinates of the turning points.We put these values of x into the equation of the graph to find the y – coordinates of the tuning points.
We differentiate
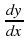 to find
to find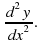 We put the values of x from 1. into the expression for
We put the values of x from 1. into the expression for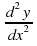 to find a value: if this value is positive then the stationary point is a minimum. If this value is negative then this stationary point is a maximum. If this value is zero then we can find y values a little either side of the stationary point and do a 3 point sketch to determine if a maximum, minimum.
to find a value: if this value is positive then the stationary point is a minimum. If this value is negative then this stationary point is a maximum. If this value is zero then we can find y values a little either side of the stationary point and do a 3 point sketch to determine if a maximum, minimum.
Example:![]()
Find the turning points and determine their nature.
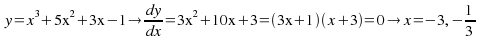
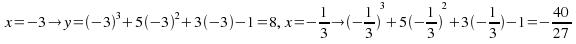
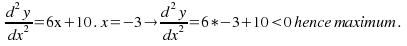
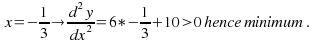 This is shown below.
This is shown below.