Suppose we have a 200m of fence to close of part of a field which backs onto a hedge. The hedge and fence are to form a rectangle. This is shown in the diagram, with the green rectangle being the hedge.
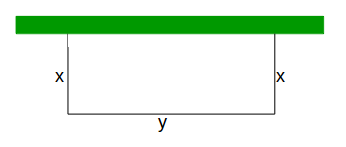
\[2x+y\]
so \[2x+y=200\]
.The enclosed
\[xy\]
.The pronlem is now 'maximise
\[xy\]
subject to \[2x+y=200\]
'.We can substitute
\[2x+y=200\]
into \[A(x,y)\]
to obtain an equation in terms of \[x\]
, which we can then maximise by completing the square.\[2x+y=200 \rightarrow y=200-2x \rightarrow A(x)=x(200-2x)=200x-2x^2\]
.Now complete the square.
\[100-2x^2=-2(x^2-100x)=-2((x-50)^2-50^2)=2 \times 50^2-2(x-50)^2=5000\]
.The maximum value of
\[A\]
is 5000, when \[x=50\]
/