Minimum Time to Move Between Fixed Points Through a Point Moving Along x Axis
\[x\]
axis between points A and B.Line segments joint to point P to points R and S as shown, and the lines PR and PS make angles \[\theta\]
and \[\phi\]
with the positive and negative \[y\]
axes respectively. How can you find the minimum time to move from R to Q?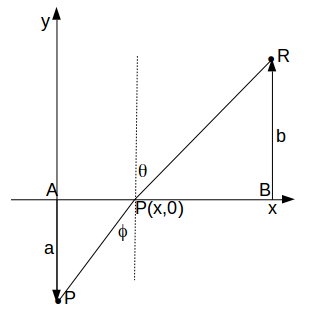
\[tan \theta =\frac{AB-x}{b} \rightarrow sec^2 \theta \frac{d \theta}{dx}=- \frac{1}{b} \rightarrow \frac{d \theta}{dx}=- \frac{cos^2 \theta}{b}\]
\[tan \phi =\frac{x}{a} \rightarrow sec^2 \phi \frac{d \phi}{dx}= \frac{1}{a} \rightarrow \frac{d \phi}{dx}= \frac{cos^2 \phi}{a}\]
Then
\[\frac{d \theta}{d \phi}=\frac{\frac{d \theta}{dx}}{\frac{d \phi}{dx}}=\frac{- \frac{cos^2 \theta}{b}}{ \frac{cos^2 \phi}{a}}=- \frac{a cos^2 \theta}{b cos^2 \phi}\]
Let a particle move from R to P with speed
\[v_1\]
and from P to Q with speed \[v_2\]
.The time taken to move from R to P is
\[t_1=\frac{b}{v_1 cos \theta}\]
.The time taken to move from P to Q is
\[t_2=\frac{a}{v_2 cos \phi}\]
.The time taken to move from R to Q is then
\[T=\frac{b}{v_1 cos \theta}+ \frac{a}{v_2 cos \phi}\]
.\[\begin{equation} \begin{aligned} \frac{dT}{d \theta}&= \frac{b sec \theta tan \theta}{v_1 } + \frac{a}{v_2 sec \phi tan \phi} \frac{d \phi}{d \theta} \\ &= \frac{b sec \theta tan \theta}{v_1 } + \frac{a}{v_2 sec \phi tan \phi} (- \frac{b cos^2 \phi}{a cos^2 \theta}) \\ &= b sec^2 \theta (\frac{sin \theta}{v_1}-\frac{sin \phi}{v_2}) =0 \end{aligned} \end{equation}\]
.Hence
\[\frac{sin \theta}{v_1}-\frac{sin \phi}{v_2} =0 \rightarrow \frac{sin \theta}{sin \phi}=\frac{v_1}{v_2}\]
is a condition for what is obviously a minimum time.