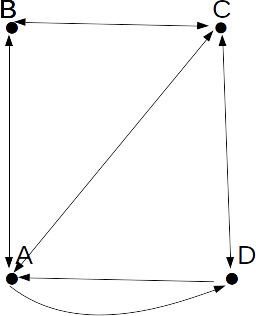
| A | B | C | D | |
| A | 0 | 1 | 1 | 1 |
| B | 1 | 0 | 1 | 0 |
| C | 1 | 1 | 0 | 1 |
| D | 1 | 0 | 1 | 0 |
\[M= \left( \begin{array}{cccc} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{array} \right) \]
is the matrix representing the connectedness of the netweok.\[M^2= \left( \begin{array}{cccc} 3 & 1 & 2 & 1 \\ 1 & 2 & 1 & 2 \\ 2 & 1 & 3 & 1 \\ 1 & 2 & 1 & 2 \end{array} \right), \; M^3
= \left( \begin{array}{cccc} 6 & 5 & 5 & 5 \\ 2 & 4 & 2 & 4 \\ 5 & 5 & 4 & 5 \\ 5 & 2 & 5 & 2 \end{array} \right) \]
\[M^2\]
and \[M^3\]
give the number of feedback routes - along the main diagonal - with 1 and 2 intermediat vertices repectively. The entry in the 1st row, 1st column of \[M\]
is 3, so there are three feedback routes with 1 intermediate vertex. These are A-B-A, A-C-A and A-D-A.