Summary
Algebraic fractions involve polynomials, usually expressed in terms of a polynomial
divided by other polynomials in– they may need to be added, subtracted, multiplied or divided. The rules are the same as for ordinary fractions:
To add or subtract, we make a common denominator then subtract the numerators.
To multiply, we just “multiply across”, so that the end result is
To divide, turn the dividing, second fraction, upside down, and multiply.
Adding Algebraic Fractions
The new denominator is
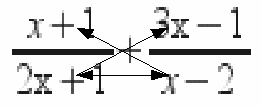
In the diagram above the arrows indicate multiplication
To illustrate, I will expand the brackets in the numerator and add
The numerator
can be factorised into
There is a common factor
in numerator and denominator which can be cancelled.
Subtracting Algebraic Fractions
The new denominator is
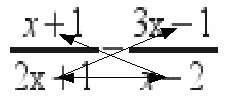
In the diagram above the arrows indicate multiplication
To illustrate, I will expand the brackets in the numerator and subtract
There is no common factor.
Multiplying Algebraic Fractions
Just multiply across
There are no common factors so we cannot cancel.
Dividing Algebraic Fractions
Turn the second, dividing fraction upside down and multiply as above:
