|
Shape |
Picture |
Number of Sides |
Interior Angle |
Sum of Interior Angles |
Exterior Angle |
|
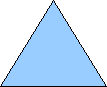
Triangle |
|
3 |
60 |
180 |
120 |
|
Square |
|
4 |
90 |
360 |
90 |
|
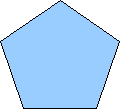
Pentagon |
|
5 |
108 |
540 |
72 |
|
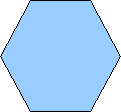
Hexagon |
|
6 |
120 |
720 |
60 |
|
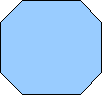
Octagon |
|
8 |
135 |
1080 |
45 |
|
n- agon |
|
|
|
|
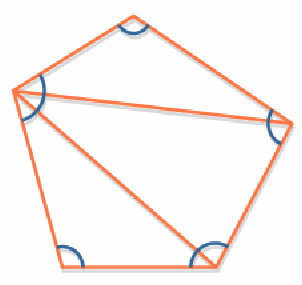
To see why the angles in a triangle add to![]() notice that a triangle has three sides so n=1 and the angles add to 180, a square can be cut into two triangles, each with internal angles 180, so all the internal angles of both triangles sum to 360. Consider the pentagon below. It is cut into three triangle, each with internal angles that sum to 360, so the internal angles of a pentagon sum to 3*180 =540.
notice that a triangle has three sides so n=1 and the angles add to 180, a square can be cut into two triangles, each with internal angles 180, so all the internal angles of both triangles sum to 360. Consider the pentagon below. It is cut into three triangle, each with internal angles that sum to 360, so the internal angles of a pentagon sum to 3*180 =540.