Scalar quantities are quantities that need only a number to describe them fully. Examples include:
mass, speed, distance, power, energy.
Vector quantities are quantities that have both number and direction. Examples include: velocity, displacement, force, acceleration.
Some scalar quantities have commonly used vector versions. For example, we may use either speed or velocity in conversation, and when we speak of distance, which is a scalar, we usually mean the distance from somewhere to somewhere else, which makes it a vector.
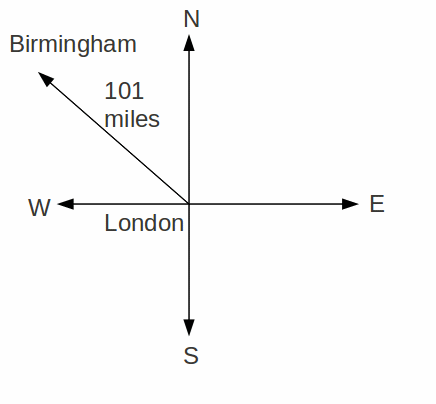
The distance from London to Birmingham is 101 miles, and 101 miles is a scalar, but to travel from London to Birmingham we can't start from London and go in any direction – we have to travel north west, and this pairing of distance with direction defines a vector.
If we take 2 hours to travel from London to Birmingham, the speed is![]() and this is a scalar, but we must travel in the direction north west, and this pairing of speed with direction defines a vector.
and this is a scalar, but we must travel in the direction north west, and this pairing of speed with direction defines a vector.
|Scalars can be added or subtracted with no complications. Masses of 3Kg and 5Kg together make a mass of 8Kg, but we have to be careful about adding vectors. Adding a force of 3N directed North to a force of 5N directed north east is best illustrated by drawing a triangle.
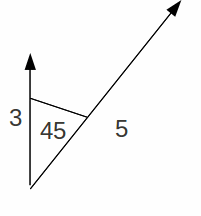
We construct a parallelogram as shown.
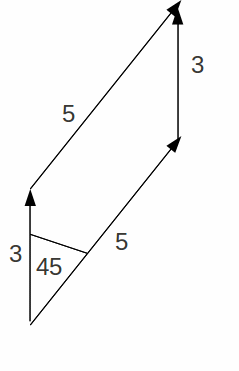
Now draw in the diagonal so that it represents the sum of the two vectors.
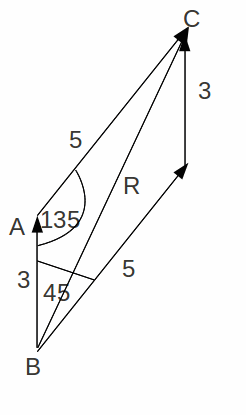
We can use the triangle ABC to find the resultant R using the cosine rule.![]()
![]()
We can also find the bearing, given by the angle![]() using the sine rule:
using the sine rule:
![]()
![]()