If a group is finite we can modify The Internal Direct Product Theorem as below.
The Internal Direct Product Theorem
If![]() and
and![]() are subgroups of a group
are subgroups of a group![]() then
then![]() is an isomorphism if and only if the following conditions are satisfied:
is an isomorphism if and only if the following conditions are satisfied:
-
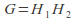 (if
(if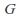 is finite then
is finite then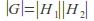 ).
). -
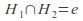 (If
(If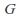 is finite then
is finite then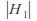 and
and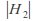 are coprime).
are coprime). -
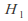 and
and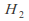 are normal subgroups of
are normal subgroups of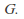
Proof:
![]() so we must prove that all the
so we must prove that all the![]() are distinct. Suppose not, so that
are distinct. Suppose not, so that![]() but then
but then![]() The left hand side is in
The left hand side is in![]() and the right hand side is in
and the right hand side is in![]() so both are equal to e since the intersection is trivial so
so both are equal to e since the intersection is trivial so![]() and
and ![]() All the
All the![]() are distinct therefore and
are distinct therefore and![]() This implies that
This implies that![]() is one to one. Since
is one to one. Since![]()
![]() is also onto.
is also onto.
If![]() are subgroups of G,
are subgroups of G,![]() is a subgroup of both
is a subgroup of both![]() and
and![]() By Lagrange's Theorem,
By Lagrange's Theorem,![]() must divide both
must divide both![]() and
and![]() but these are coprime so
but these are coprime so![]() hence
hence![]()
All the conditions of the internal direct product theorem are met.
Example:![]() and
and![]()
1 is satisfied since 6=2*3.
2 is satisfied since![]()
![]() is abelian so all subgroups are normal and 3 is satisfied.
is abelian so all subgroups are normal and 3 is satisfied.