A function![]() is one to one or injective if
is one to one or injective if![]() implies
implies![]() The one to one property is important because any one to one function has an inverse. This mean that
The one to one property is important because any one to one function has an inverse. This mean that![]() has only one value for x' in Im f.
has only one value for x' in Im f.
To say a function is injective implies nothing about the continuity or differentiability of the function. The function may be defined for a discrete set of numbers, for one or several intervals or a combination of discrete numbers and intervals, or for all real numbers, but if the function is continuous or differentiable it must either be:
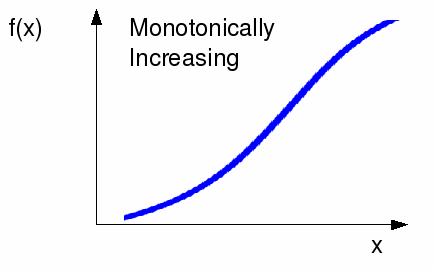
Monotonically increasing, so that![]() and if
and if![]() then it is zero at a point and not on an interval.
then it is zero at a point and not on an interval.
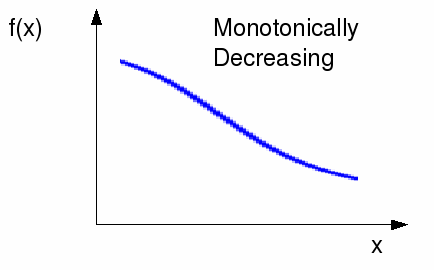
Monotonically decreasing, so that![]() and if
and if![]() then it is zero at a point and not on an interval.
then it is zero at a point and not on an interval.
The function below is not monotonically increasing or decreasing so is not one to one.
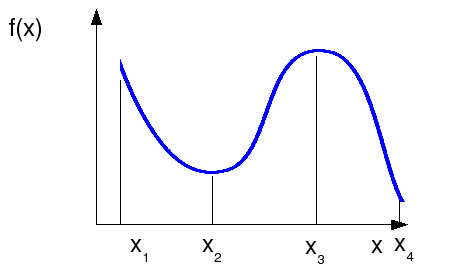
We can always make a function one to one by restricting the domain or set of x values that it can take to a set on which the function is monotonic (for a continuous function) or by throwing out 'surplus' values of x from the domain which return the same values of x. The function f above can be made one to one by restricting it to one of the ranges![]()