Definition: Let![]() be a subset of
be a subset of![]() and let
and let![]() be a sequence of functions defined on
be a sequence of functions defined on![]() We say that
We say that![]() converges pointwise on
converges pointwise on![]() if
if ![]() exists for each point
exists for each point![]()
This means that![]() is a real number that depends only on
is a real number that depends only on![]()
If![]() is pointwise convergent then the function defined by
is pointwise convergent then the function defined by![]()
for every![]() is called the pointwise limit of the sequence
is called the pointwise limit of the sequence![]()
More formally, given any![]() and
and ![]() there exists a natural number
there exists a natural number![]() depending only on
depending only on![]() and
and![]() such that
such that
![]() for every
for every![]()
Definition Let![]() be a subset of
be a subset of![]() and let
and let![]() be a sequence of real valued functions defined on
be a sequence of real valued functions defined on![]() Then
Then![]() converges uniformly to
converges uniformly to![]() if given any
if given any![]() there exists a natural number
there exists a natural number![]() such that
such that![]() for every
for every![]()
![]() depends only on
depends only on![]() so uniform convergence implies pointwise convergence., but the converse is not true.
so uniform convergence implies pointwise convergence., but the converse is not true.
Example:![]()
As![]() for each
for each![]() so
so ![]() converges pointwise to zero.
converges pointwise to zero.
Suppose now that![]() and
and![]() then
then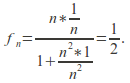 and
and![]() so
so![]() is not uniformly convergent.
is not uniformly convergent.