The Bolzano Weierstrass Theorem
We need first a definition
Definition Let![]() be a set of real numbers. A real number
be a set of real numbers. A real number![]() is an accumulation point of
is an accumulation point of![]() if and only if every neighbourhood of
if and only if every neighbourhood of![]() contains infinitely many points of
contains infinitely many points of![]()
For example 0 is an accumulation point of the set![]() since
since![]() contains all
contains all![]() for
for![]() Note the accumulation point need not belong to the set.
Note the accumulation point need not belong to the set.
The Bolzano Weierstrass Theorem
Every bounded infinite set of numbers has at least one accumulation point.
Proof: Let![]() be a bounded infinite set. Since
be a bounded infinite set. Since![]() is bounded, there are real numbers
is bounded, there are real numbers![]() and %beta such that
and %beta such that![]() If
If![]() is the midpoint of this interval, then at least one of the sets
is the midpoint of this interval, then at least one of the sets![]() must contain an infinite number of members of
must contain an infinite number of members of![]() Choose one with this property and call it
Choose one with this property and call it![]() If
If![]() is the midpoint of this interval, then at least one of the sets
is the midpoint of this interval, then at least one of the sets![]() must contain an infinite set of members of
must contain an infinite set of members of![]() Choose one with this property and call it
Choose one with this property and call it![]() Continuing in this fashion we obtain for each positive integer
Continuing in this fashion we obtain for each positive integer![]() a closed interval
a closed interval![]() with the following properties:
with the following properties:
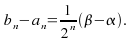
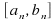 contains infinitely many points of
contains infinitely many points of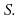
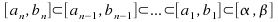
Since![]() for all
for all![]() the set
the set![]() is bounded. Let
is bounded. Let![]() is the desired accumulation point. We need to show that every neighbourhood of
is the desired accumulation point. We need to show that every neighbourhood of![]() contains infinitely many points of
contains infinitely many points of![]() Let
Let![]() be any neighbourhood of
be any neighbourhood of![]() then there exists
then there exists![]() such that
such that![]() Now
Now![]() is not an upper bound for
is not an upper bound for![]() since
since![]() is the least upper bound hence there is a positive number
is the least upper bound hence there is a positive number![]() such that
such that![]() If
If![]() then by the construction above
then by the construction above![]() Each interval
Each interval![]() contains infinitely many points of
contains infinitely many points of![]() so the proof would be complete if
so the proof would be complete if![]() could be found such that
could be found such that![]() As noted above,
As noted above,![]() for
for ![]() so it will be enough to choose
so it will be enough to choose![]() large enough so that
large enough so that![]() and
and![]() then
then![]() Thus
Thus![]() contains
contains![]() hence
hence![]() contains infinitely many members of
contains infinitely many members of![]() and
and![]() is an accumulation point of
is an accumulation point of![]()
The boundedness of the set is necessary because for example![]() is infinite but has no accumulation points.
is infinite but has no accumulation points.