Jordan’s Lemma describes the behaviour of a contour integral on the semicircular arc or radius![]() (excluding the real axis) in the upper half of the complex plane as the radius of the semicircle tends to infinity.
(excluding the real axis) in the upper half of the complex plane as the radius of the semicircle tends to infinity.
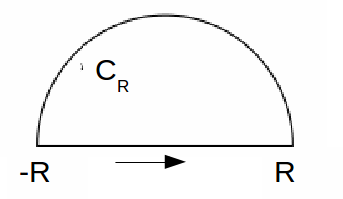
Jordan's Lemma
If the only singularities of F(z) are simple and![]() as
as![]() then
then
![]()
if![]() and |F (z)| → 0 as R → ∞.
and |F (z)| → 0 as R → ∞.
Proof: Since![]() is the semi-circle
is the semi-circle![]() and
and![]()
![]()
![]()
![]()
Now![]() in the upper half plane, and
in the upper half plane, and![]() tends to zero faster than any power of R increases if
tends to zero faster than any power of R increases if![]() so by splitting the semicircular contour into three parts,
so by splitting the semicircular contour into three parts,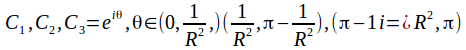
we obtain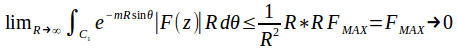 andd similarly for
andd similarly for![]() and for
and for![]() since as stated,
since as stated,![]() tends to 0 faster than any power of
tends to 0 faster than any power of![]() increases as
increases as![]() rightarrow infinity , so
rightarrow infinity , so![]()
When![]() if
if![]() or a rational function of
or a rational function of![]()
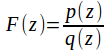 with the degree of the denominator higher than the degree of the numerator can all be used.
with the degree of the denominator higher than the degree of the numerator can all be used.
If![]() then a modification is needed. The degree of the denominator must be at least two greater than the degree of the nureator.
then a modification is needed. The degree of the denominator must be at least two greater than the degree of the nureator.
If![]() then we can still apply the Lemma by taking our contour in the lower half plane.
then we can still apply the Lemma by taking our contour in the lower half plane.