Theorem
Let![]() be a function with domain
be a function with domain![]() and suppose that
and suppose that![]() is a limit point of
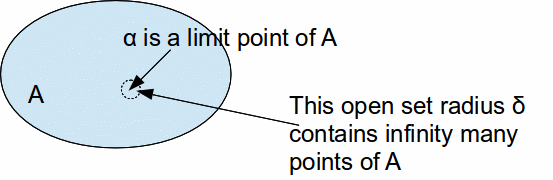
is a limit point of![]() so that every open neighbourhood of
so that every open neighbourhood of![]() contains infinitely many points of
contains infinitely many points of![]()
the following statements are equivalent:
-
f is continuous at
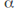
-
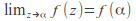
Proof
Suppose that![]() is continuous at
is continuous at![]() If
If![]() is any sequence in
is any sequence in![]() with
with![]() then it follows that for
then it follows that for![]() we can find
we can find![]() such that
such that![]() implies
implies![]()
Hence![]()
Conversely suppose that![]() If
If ![]() is any sequence in
is any sequence in![]() with
with![]() and
and![]() is the subsequence of
is the subsequence of![]() consisting of those terms different from
consisting of those terms different from![]() then
then![]() since
since![]() and
and![]()
The remaining subsequence![]() of
of![]() satisfies
satisfies![]() for all
for all![]() so
so![]() so
so![]() and
and![]() is continuous at
is continuous at![]()