Confidence Intervals for the Coefficients of Regression Lines
For a regression line![]() the
the![]() are themselves random variables. To find estimates for the
are themselves random variables. To find estimates for the![]() we form an expression for the sum of the error terms squared:
we form an expression for the sum of the error terms squared:![]() We minimise this sum by allowing the
We minimise this sum by allowing the![]() to vary. Differentiating each with respect to each
to vary. Differentiating each with respect to each![]() leads to the following system of equations:
leads to the following system of equations:
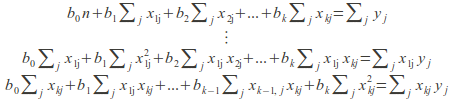
Because the regression line![]() is linear in the b-i the equations above are linear too. We can solve this system of linear equations to solve for the
is linear in the b-i the equations above are linear too. We can solve this system of linear equations to solve for the![]() these solutions are labelled
these solutions are labelled![]() The
The![]() are themselves random variables because they are functions of the random variables
are themselves random variables because they are functions of the random variables![]() Because the equations are linear, the
Because the equations are linear, the![]() are normally distributed with corresponding standard deviation
are normally distributed with corresponding standard deviation![]() We can then construct confidence intervals for each
We can then construct confidence intervals for each![]()
![]()
Typically we want to test whether 0 is in the interval. If it is, then at the significance level of the test, there is no evidence of a correlation between![]() and
and![]()
Much of the time the![]() and
and![]() are found automatically with computer packages.
are found automatically with computer packages.
Example: The table below gives data on the amount of iron, aluminium and phosphate in soil.
Observation |
|
|
|
1 | 61 | 13 | 4 |
2 | 175 | 21 | 18 |
3 | 111 | 24 | 14 |
4 | 124 | 23 | 18 |
5 | 130 | 64 | 26 |
6 | 173 | 38 | 26 |
7 | 169 | 33 | 21 |
8 | 169 | 61 | 30 |
9 | 160 | 39 | 28 |
10 | 244 | 71 | 36 |
11 | 257 | 112 | 65 |
12 | 333 | 88 | 62 |
13 | 199 | 54 | 40 |
A computer package returns the results:
Parameter | Estimate, | Estimated standard deviation, |
| -7.35100 | 3.48500 |
| 0.11273 | 0.02969 |
| 0.34900 | 0.07131 |
A 99% confidence interval for![]() is then, with
is then, with![]()
![]()
A 99% confidence interval for![]() is, with
is, with![]()
![]()