Theorem
If![]() are Cauchy sequences in a metric space
are Cauchy sequences in a metric space![]() such that
such that![]() for
for![]() then
then
-
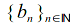 is also a Cauchy sequence
is also a Cauchy sequence -
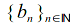 converges to
converges to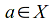 if and only if
if and only if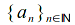 converges to
converges to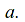
Proof
For 1:
Applying the triangle inequality,![]()
Let![]() We can find
We can find![]() such that
such that![]()
Since![]() is Cauchy, there exists
is Cauchy, there exists![]() such that
such that![]()
Now let![]() we get
we get![]() hence
hence ![]() is Cauchy.
is Cauchy.
For 2:
Using the triangle theorem again gives![]()
Hence,![]() but
but![]()
If![]() then
then![]() and
and![]()
Similarly, if![]() then
then![]()