If![]() is a group,
is a group,![]() is a subgroup of
is a subgroup of![]() and
and![]() then
then
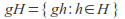 is a left coset of
is a left coset of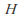 in
in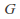
-
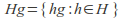 is a right coset of
is a right coset of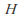 in
in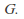
If![]() or equivalently
or equivalently![]() for all
for all![]() then
then![]() is a normal subgroup of
is a normal subgroup of![]() The left and right cosets coincide and the set of cosets forms a group with the group operation defined by
The left and right cosets coincide and the set of cosets forms a group with the group operation defined by![]() For
For![]() under the operation addition modulo 3, the cosets of
under the operation addition modulo 3, the cosets of![]() are
are![]() and
and![]() If G is abelian then all subgroups are normal.
If G is abelian then all subgroups are normal.
![]() if and only if
if and only if![]() is an element of H since as H is a subgroup, it must be closed and must contain the identity.
is an element of H since as H is a subgroup, it must be closed and must contain the identity.
Any two left cosets of![]() in
in![]() are either identical or disjoint — i.e., the left cosets form a partition of
are either identical or disjoint — i.e., the left cosets form a partition of![]() such that every element of
such that every element of![]() belongs to one and only one left coset. In particular the identity is in precisely one coset, and that coset is
belongs to one and only one left coset. In particular the identity is in precisely one coset, and that coset is![]() itself since this is also the only coset that is a subgroup.
itself since this is also the only coset that is a subgroup.
The left cosets of![]() in
in![]() are the equivalence classes under the equivalence relation on
are the equivalence classes under the equivalence relation on![]() given by
given by![]() if and only if
if and only if![]() and similarly for right cosets.
and similarly for right cosets.
All left cosets and all right cosets have the same order (number of elements, or cardinality in the case of an infinite H), equal to the order of H (because H is itself a coset). Furthermore, the number of left cosets is equal to the number of right cosets and is known as the index of H in G, written as![]() Lagrange's theorem allows us to compute the index in the case where
Lagrange's theorem allows us to compute the index in the case where![]() and
and![]() are finite, as per the formula:
are finite, as per the formula: