A field is a set![]() that is a commutative group with respect to two compatible operations, addition and multiplication, with "compatible" being formalized by distributivity, and the caveat that the additive identity (0) has no multiplicative inverse (one cannot divide by 0).
that is a commutative group with respect to two compatible operations, addition and multiplication, with "compatible" being formalized by distributivity, and the caveat that the additive identity (0) has no multiplicative inverse (one cannot divide by 0).
The most common way to formalize this is by defining a field as a set together with two operations, usually called addition and multiplication, and denoted by![]() and
and![]() respectively, such that the following axioms hold;
respectively, such that the following axioms hold;
- Closure of
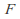 under addition and multiplication
under addition and multiplication - For all
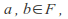
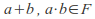 (or more formally,
(or more formally,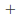 and
and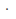 are binary operations on
are binary operations on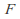 ).
). - Associativity of addition and multiplication
- For all
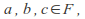
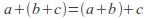 and
and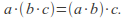
- Commutativity of addition and multiplication
- For all
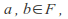
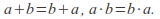
- Additive and multiplicative identity
- There exists an element of
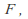 called the additive identity element and denoted by 0, such that for all
called the additive identity element and denoted by 0, such that for all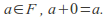 Likewise, there is an element, called the multiplicative identity element and denoted by 1, such that for all
Likewise, there is an element, called the multiplicative identity element and denoted by 1, such that for all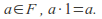 The additive identity and the multiplicative identity may not be the same.
The additive identity and the multiplicative identity may not be the same. - Additive and multiplicative inverses
- For every
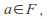 there exists
there exists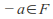 such that
such that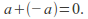 Similarly, for any
Similarly, for any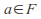 other than 0, there exists an element
other than 0, there exists an element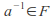 such that
such that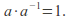 (The elements
(The elements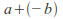 and
and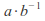 are denoted
are denoted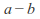 and
and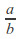 respectively.) In other words subtraction and division operations exist.
respectively.) In other words subtraction and division operations exist. - Distributivity of multiplication over addition
- For all
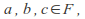
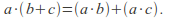
Note that all but the last axiom are exactly the axioms for a commutative group, while the last axiom is a compatibility condition between the two operations.
Examples:![]() are all fields as is
are all fields as is![]() for n prime. The tables below are for a finite field with four elements.
for n prime. The tables below are for a finite field with four elements.
| 0 | 1 | A | B |
| 0 | 1 | A | B | |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | A | B | |
1 | 0 | 1 | A | B | 1 | 1 | 0 | B | A | |
A | 0 | A | B | 1 | A | A | B | 0 | 1 | |
B | 0 | B | A | 1 | B | B | A | 1 | 0 |