Let![]() be a set and let
be a set and let![]() be a group who elements act on the set
be a group who elements act on the set![]() A left group action is a function
A left group action is a function![]() such that:
such that:
-
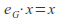 for all
for all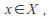 where
where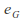 is the identity element in
is the identity element in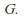
-
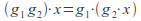 for all
for all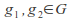 and
and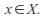
Right actions are similarly defined.
From these two axioms, it follows that for every![]() the function which maps
the function which maps![]() to
to![]() is a bijective map from
is a bijective map from![]() to
to![]() Therefore, one may alternatively and equivalently define a group action of
Therefore, one may alternatively and equivalently define a group action of![]() on
on![]() as a group homomorphism from
as a group homomorphism from![]() to the set of all bijective maps from
to the set of all bijective maps from![]() to
to![]()
If a group action![]() is given, we also say that
is given, we also say that![]() acts on the set
acts on the set![]() or
or![]() is a
is a![]() - set.
- set.
-
Every group
 acts on itself in two natural ways:
acts on itself in two natural ways: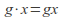 for all
for all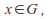 or
or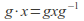 for all
for all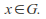
-
The symmetric group
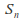 and its subgroups act on the set
and its subgroups act on the set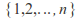 by permuting its elements.
by permuting its elements. -
The symmetry group of a polyhedron acts on the set of vertices of that polyhedron.
-
The symmetry group of any geometrical object acts on the set of points of that object.
-
The automorphism group of a vector space (or graph, or group, or ring...) acts on the vector space (or set of vertices of the graph, or group, or ring...).
-
The Matrix groups
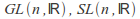 and
and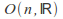 act on
act on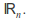
-
The Galois group and every subgroup of a field extension
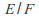 acts on the bigger field
acts on the bigger field
-
The additive group of the real numbers
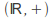 acts on the phase space of systems in classical mechanics (and in more general dynamical systems): if
acts on the phase space of systems in classical mechanics (and in more general dynamical systems): if and
and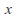 is in the phase space, then
is in the phase space, then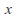 describes a state of the system, and
describes a state of the system, and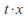 is defined to be the state of the system
is defined to be the state of the system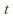 seconds later if
seconds later if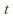 is positive or
is positive or seconds ago if
seconds ago if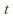 is negative.
is negative.