The axioms (basic rules) for a group G are:
-
CLOSURE: If
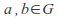 then
then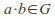 where
where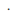 is the rule for composing elements of the group.
is the rule for composing elements of the group. -
ASSOCIATIVITY: If
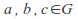 then
then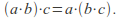
-
IDENTITY: There is an element
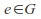 such that for any element a of the group
such that for any element a of the group 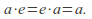 The identity is unique.
The identity is unique. -
INVERSES: For any element
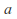 of the group there is an unique element
of the group there is an unique element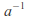 such that
such that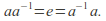
Closure
If![]() then
then![]() is also in the group.
is also in the group.
For a system to be a group the group operation must hold for any pair of elements in the group and the result of the operation must be an element of the group. The set of negative integers, for example, is not closed under multiplication because the product of two negative integers is not a negative integer.
Associativity
If![]() then
then![]()
Addition and multiplication of real numbers is associative but not subtraction and division. For example![]() but
but ![]()
Identity
There is an element![]() of the group such that for any element
of the group such that for any element![]() of the group
of the group ![]()
Cross product of three dimensional vectors is an example of a binary operation that does not have an identity element. Since the cross product of![]() with any other vector is either the zero vector or a vector perpendicular to
with any other vector is either the zero vector or a vector perpendicular to![]() there can be no vector
there can be no vector![]() with
with![]() (otherwise
(otherwise![]() would be perpendicular to itself).
would be perpendicular to itself).
Inverses
For any element![]() of the group there is an element
of the group there is an element![]() such that
such that![]()
In order for an operation to satisfy the axiom for inverses the operation must have an identity element. Any vector does not have an inverse under the cross product operation since there is no identity.