If![]() is a normal subgroup of
is a normal subgroup of![]() then the coset space
then the coset space![]() with the binary operation
with the binary operation
![]()
for all![]() belonging to
belonging to![]() is a group. The identity element of this group is the trivial coset
is a group. The identity element of this group is the trivial coset![]()
Let G be a group and let H be a subgroup of G. The following statements are equivalent:
-
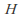 is a normal subgroup of
is a normal subgroup of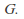
-
For all
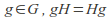 (The left and right cosets are identical)
(The left and right cosets are identical) -
Coset multiplication is well-defined that is if
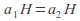 and
and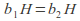 then
then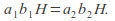 Once this is established the rule for multiplication of cosets
Once this is established the rule for multiplication of cosets 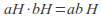 follows.
follows.
Proof
![]() If
If![]() is normal in
is normal in![]() and and
and and![]() then
then![]() so
so![]()
![]() Suppose
Suppose![]() for all
for all![]() Suppose
Suppose![]() Then
Then![]()
![]() Suppose coset multiplication is well defined. Let
Suppose coset multiplication is well defined. Let![]()
![]() so
so![]() and
and ![]() so
so![]() is normal in
is normal in![]()
Now the main result: If![]() is a normal subgroup of
is a normal subgroup of![]() the set of cosets
the set of cosets![]() becomes a group under coset multiplication.
becomes a group under coset multiplication.
Proof
For associativity, note that
![]() and
and![]()
![]()
Hence,![]() is the identity for coset multiplication.
is the identity for coset multiplication.
Finally![]() so
so![]() for
for![]() and every coset (element of the set
and every coset (element of the set![]() has an inverse hence
has an inverse hence![]() is a group, called the quotient group of
is a group, called the quotient group of![]() by
by![]()