Simple Groups
A simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated. In a very real sense, the simple groups are the fundamental building blocks of all groups. If the group is finite, then eventually one arrives at uniquely determined simple groups by the Jordan–Hölder theorem (any two composition series of a given group have the same length and the same factors, up to permutation and isomorphism). All finite simple groups have now been classified.
The cyclic group![]() of congruence classes modulo 3 is simple. If
of congruence classes modulo 3 is simple. If![]() is a subgroup of this group, its order must be a divisor of the order of
is a subgroup of this group, its order must be a divisor of the order of![]() 1 or 3 so is the trivial group or the whole group. The group
1 or 3 so is the trivial group or the whole group. The group![]() is not simple.
is not simple.![]() is a normal (since
is a normal (since![]() is abelian) . Similarly, the additive group
is abelian) . Similarly, the additive group![]() of integers is not simple since
of integers is not simple since![]() is a subgroup.
is a subgroup.
The reasoning above shows that the only simple abelian groups are the cyclic groups of prime order. The classification of non - abelian simple groups is not as trivial. The smallest non - abelian simple group is the alternating group![]() of order 60, and every simple group of order 60 is isomorphic to
of order 60, and every simple group of order 60 is isomorphic to![]()
Finite simple groups are classified as lying in one of 18 families, or being one of 26 exceptions:
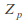 – cyclic group of prime order
– cyclic group of prime order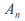 – the alternating group of order
– the alternating group of order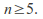 The alternating groups may be considered as groups of Lie type over the field with one element, which unites this family with the next, and thus all families of non-abelian finite simple groups may be considered to be of Lie type.
The alternating groups may be considered as groups of Lie type over the field with one element, which unites this family with the next, and thus all families of non-abelian finite simple groups may be considered to be of Lie type.One of 16 families of groups of Lie type. The Tits group is generally considered of this form, though strictly speaking it is not of Lie type, but rather index 2 in a group of Lie type.
One of 26 exceptions, the sporadic groups, of which 20 are subgroups or subquotients of the monster group and are referred to as the "Happy Family", while the remaining 6 are referred to as pariahs.