The quadratic equation![]() does not factorise. This means that it has no fractional roots of the form
does not factorise. This means that it has no fractional roots of the form![]() where a and b are whole numbers. In fact it has no real roots because the discriminant
where a and b are whole numbers. In fact it has no real roots because the discriminant![]()
The set of fractions, or rationals, is a field, labelled![]()
![]() has no rational roots.
has no rational roots.
In fact the roots are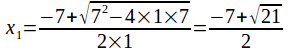 and
and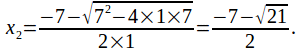
![]() is rational but
is rational but![]() is not. We cannot express the roots of the polynomial in terms of the field
is not. We cannot express the roots of the polynomial in terms of the field![]() but if we add
but if we add![]() to the field
to the field![]() we can express the roots in terms of the extended field, written
we can express the roots in terms of the extended field, written![]()
![]() is called an splitting field of the field
is called an splitting field of the field![]()
Consider the quintic equation![]() This equation factorises into
This equation factorises into![]() The first factor has root
The first factor has root![]() and
and![]() above and the second has roots
above and the second has roots![]() and
and![]() We can't express the roots of this polynomial in terms of rational fractions or even in terms of the rational fractions and
We can't express the roots of this polynomial in terms of rational fractions or even in terms of the rational fractions and![]() but we can express the roots in terms of rational fractions,
but we can express the roots in terms of rational fractions,![]() and
and![]() This field is written
This field is written![]() and includes all expressions of the form
and includes all expressions of the form![]() or
or ![]() where
where![]()
We can always extend![]() to include the roots of a polynomial in this way. We can find a splitting field for any polynomial.
to include the roots of a polynomial in this way. We can find a splitting field for any polynomial.