The Center of a Group

The center of a groupwrittenis the set of elementsthat satisfyfor all– that this, they commute with all

The center is a subgroup ofand is abelian, since every element ofcommutes with every element ofso also commutes with every element ofWe can prove thatis a subgroup ofusing the subgroup axioms.

S1:implyIfthenandfor all so

S2:for allso

S3:impliesimpliesfor allso

As a subgroup,is normal sincefor allsoand The quotient groupis well defined.

A groupis abelian if and only ifAt the other extreme, a group is said to be centerless if

Consider the map

This is a group homomorphism, and its kernel is preciselysince ifIts image is called the inner automorphism group ofdenoted

Examples

• The center of a nonabelian simple group is trivial, since simple groups have no nontrivial normal subgroups.

• The center of the dihedral group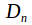is trivial when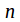is odd. When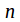is even, the center consists of the identity element together with the half rotation.

• The center of the quaternion group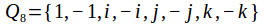is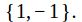

• The center of the symmetric group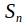is trivial for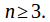

• The center of the alternating group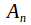is trivial for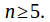

• The center of the general linear group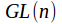is the collection of scalar matrices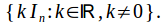

• The center of the orthogonal group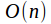is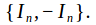

• The center of the multiplicative group of non-zero quaternions is the multiplicative group of non-zero real numbers.

• Using the class equation one can prove that the center of any non-trivial finite p-group is non-trivial.

• If the quotient group G / Z(G) is cyclic, G is abelian.