A conservation law is the statement that a given quantity can be neither created nor destroyed but may merely move. That leads to the statement :
The total rate of outflow from some region must equal the rate of decrease of that quantity located within that region.
Suppose we have a cylindrical surface, such that gas can flow in and out through the ends but not through the sides.
Suppose![]() denotes the density of a gas at time
denotes the density of a gas at time![]() for
for![]() Thus at any time
Thus at any time![]() the total mass of gas present in the region
the total mass of gas present in the region![]() is given by
is given by
![]()
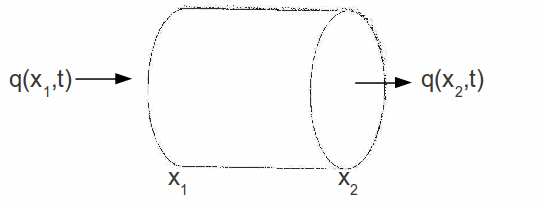
Let us denote by![]() and
and![]() the mass inflow/outflow of the gas at the ends
the mass inflow/outflow of the gas at the ends![]() and
and![]() respectively.
respectively.
The rate of change of mass of gas in the region between![]() and
and![]() is given by
is given by![]()
![]() and
and![]() are held fixed and since
are held fixed and since![]()
By adding these we obtain![]()
In higher dimensions, we obtain![]()
This is the continuity equation. The rate of flow of mass of gas out of a surface element of area![]() is
is![]() We can write the continuity equation as
We can write the continuity equation as![]() The region of integration
The region of integration![]() can be chosen arbitrarily, and since any continuous function with integral zero over an arbitrary region must be the zero function, hence
can be chosen arbitrarily, and since any continuous function with integral zero over an arbitrary region must be the zero function, hence![]()