To illustrate the method of characteristics consider the partial differential equation for![]()
![]()
Obviously, this is in fact an ODE. The solution is found by integration with respect
to![]() and reads
and reads![]() where
where![]() is an arbitrary function of
is an arbitrary function of![]()
![]() is uniquely determined by fixing
is uniquely determined by fixing![]() along the line
along the line![]() or any curve in the
or any curve in the![]() plane.
plane.
∂u
The initial value problem![]() and
and![]() for all
for all![]() has the unique solution
has the unique solution![]()
To find this solution we identified a curve along which the PDE becomes an ODE – the lines![]() - where
- where![]() is a constant, then solved the ODE for each
is a constant, then solved the ODE for each![]() – for each
– for each![]() there must be one initial value of
there must be one initial value of![]() given on this curve. We have used the coordinate
given on this curve. We have used the coordinate![]() to parameterise a characteristic curve and
to parameterise a characteristic curve and![]() to parameterise the different curves.
to parameterise the different curves.
We can generalize this. Consider the general semilinear PDE
![]()
First choose a characteristic curve parameterised by![]()
Definition: A characteristic curve is a curve in the![]() −plane, along which the PDE becomes an ODE. The characteristic curves, parameterised by
−plane, along which the PDE becomes an ODE. The characteristic curves, parameterised by![]() i.e.
i.e.![]() are solutions of the characteristic equations
are solutions of the characteristic equations
![]()
There is a one-parameter family of these curves which are parameterised by![]() If
If![]() then the characteristic curves can be expressed as functions y(x):
then the characteristic curves can be expressed as functions y(x):
they are solutions of the ODE :![]() obtained from
obtained from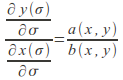 with
with![]() as the integration constant. Similarly, if
as the integration constant. Similarly, if![]() then the characteristic curves can be expressed as functions
then the characteristic curves can be expressed as functions![]() they are solutions of the ODE
they are solutions of the ODE![]()