We can prove that the sequence![]() is monotone increasing and bounded. Therefore it has a limit. The limit is in fact
is monotone increasing and bounded. Therefore it has a limit. The limit is in fact![]()
We can use the binomial theorem to write
![]()
![]() if
if![]()
![]()
hence![]() is bounded above by 3
is bounded above by 3
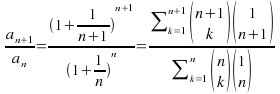
The kth term in the numerator is![]()
The kth term in the denominator is![]()
We must prove![]() then
then![]() and sequence is increasing.
and sequence is increasing.
![]()
![]() The left hand side is greater than or equal to
The left hand side is greater than or equal to![]() but the left hand side is less than 3, so
but the left hand side is less than 3, so![]() is increasing and bounded, hence converges.
is increasing and bounded, hence converges.
To find the limit, take natural logs:
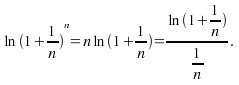
As![]() both numerator and denominator tend to zero so use L'Hopital's Rule.
both numerator and denominator tend to zero so use L'Hopital's Rule.
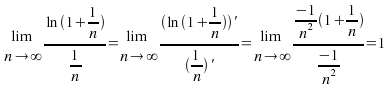
Exponentiation now gives![]() as the limit of
as the limit of![]()