We can express convergence or divergence of a power series![]() in terms of the nth root of the nth term.
in terms of the nth root of the nth term.
Theorem
Let![]() be a power series.
be a power series.
-
If the sequence
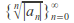 is unbounded then
is unbounded then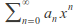 converges only for
converges only for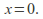
-
If the sequence
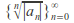 converges to zero, then
converges to zero, then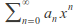 converges for all
converges for all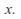
-
If the sequence
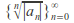 is bounded and
is bounded and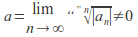 then
then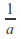 is the radius of convergence.
is the radius of convergence.
Proof
-
Choose
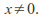 For each
For each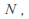 there is
there is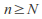 such that
such that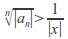 hence
hence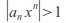 for some
for some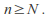 In particular
In particular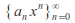 does not converge to zero for
does not converge to zero for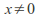 hence
hence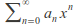 diverges for
diverges for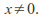
-
Suppose
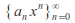 converges to zero and
converges to zero and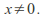 Define
Define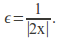 There is
There is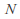 such that for
such that for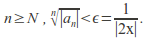 Thus for
Thus for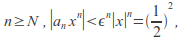 so by the comparison test,
so by the comparison test,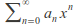 converges for all
converges for all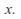
-
Suppose that
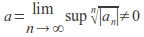 and consider any
and consider any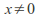 such that
such that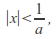 then
then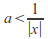 so there exist real numbers
so there exist real numbers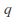 and
and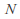 such that
such that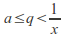 and for
and for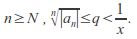 Hence for
Hence for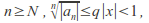 therefore
therefore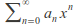 converges absolutely. To show that
converges absolutely. To show that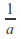 is the radius of convergence, we must show that
is the radius of convergence, we must show that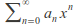 diverges for
diverges for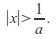 Suppose
Suppose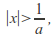 then
then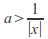 hence there are infinitely many
hence there are infinitely many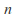 such that
such that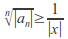 so for infinitely many
so for infinitely many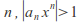 so
so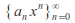 does not converge to zero and
does not converge to zero and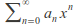 diverges.
diverges.