Differentiating Under the Integral Sign
Let R be a region and let K be a complex valued function of two variables z in R and t in [a,b] such that
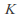 is analytic in
is analytic in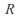 as a function of
as a function of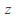 for each
for each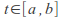
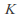 and
and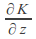 are continuous on
are continuous on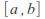 as functions of t for each
as functions of t for each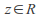
For some
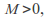
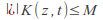 for
for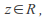
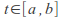
Then the function![]() with
with![]() is analytic on
is analytic on![]() and
and![]() for
for![]() (1)
(1)
Proof: Let![]() and choose a circle
and choose a circle![]() in
in![]() with centre
with centre![]() and radius
and radius![]() such that the inside of
such that the inside of![]() lies entirely in
lies entirely in![]() If
If![]() lies inside
lies inside![]() then we have by assumption 1 and Cauchy's Integral Formula,
then we have by assumption 1 and Cauchy's Integral Formula,
![]() and
and![]()
and by Cauchy's First Derivative Formula,![]() for each t in [a,b].
for each t in [a,b].
Hence, if f is given by (1) then
![]()
![]()
![]()
![]() say. We need to show that
say. We need to show that![]() as
as![]()
![]()
hence![]() as
as![]()