If![]() is a generalized circle and
is a generalized circle and![]() is an arbitrary point of the extended complex plane
is an arbitrary point of the extended complex plane![]() then
then![]() has a unique inverse point
has a unique inverse point![]() with respect to
with respect to![]()
Proof
If![]() then we may take
then we may take![]() since any point on
since any point on![]() is inverse to itself. If
is inverse to itself. If![]() let
let![]() be the extended line through
be the extended line through![]() that meets
that meets![]() at right angles at the point
at right angles at the point![]()
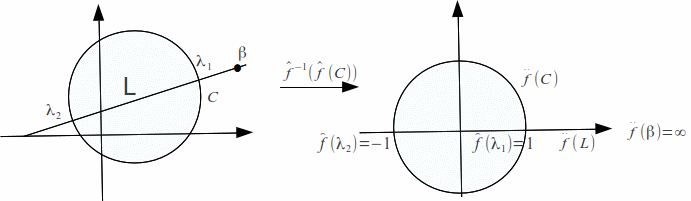
In either case let![]() be the extended mobius transformation that maps
be the extended mobius transformation that maps![]() to
to![]()
![]() to 1 and
to 1 and![]() to -1 then
to -1 then![]() is the extended real axis and it meets
is the extended real axis and it meets![]() at
at![]() and
and![]() Furthermore
Furthermore![]() meets
meets![]() at right angles at
at right angles at![]() since
since![]() preserves angles. so
preserves angles. so![]() is the unit circle. If
is the unit circle. If![]() then
then![]() and
and![]() so
so ![]() and
and![]() are inverse points with respect to
are inverse points with respect to![]() The existence of inverse points is proved.
The existence of inverse points is proved.
To prove uniqueness, if![]() and
and![]() are unique points with respect to
are unique points with respect to![]() then
then![]()
![]() and so
and so![]() must be unique.
must be unique.